Numbering Numbers, Part 2: Ordering Obliquely

haskell
diagonal argument

How do we construct an irrational number from rational ones?

Published

December 31, 2023

Modified

July 29, 2025

This post assumes you have read the previous one, which discusses the creation of sequences containing every integer, every binary fraction, and in fact, every fraction. From the fractions, we also could enumerate quadratic irrational numbers using the question-mark function.

Other Irrationals

Because rationals – and even some irrationals – can be enumerated, we might imagine that it would be nice to enumerate all irrational numbers. Unfortunately, we’re not very lucky this time.

Let’s start by making what we mean by “number” more concrete We’ve already been exposed to infinite expansions, like 1/3 in binary (and conveniently, also decimal). In discussing the question mark function, I mentioned the utility of repeating expansions as a means of accessing quadratic rationals in the Stern-Brocot tree. A general sequence need not repeat, so we can choose to treat these extra “infinite expansions” as numbers. Proving that a rational number must have a repeating expansion is difficult, but if we accept this premise, then the new non-repeating expansions are our irrationals. For example, 2 - \varphi \approx 0.381966..., which we encountered last time, is such a number.

Doing this introduces a number of headaches, the least of which is that of the definition of arithmetic on such quantities. However, we need only be concerned with the contents of these sequences to show why we can’t list out all irrationals.

Diagonalization

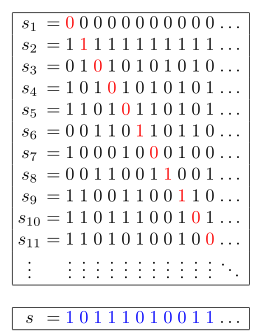
We can narrow our focus to the interval between 0 and 1, since the numbers outside this interval are their reciprocals. Now (if we agree to use base ten), “all numbers between 0 and 1” as we’ve defined them begin with “0.”, followed by an infinite sequence of digits 0-9. Suppose that we have an enumeration of every infinite sequence on this list – no sequence is left out. Cantor’s diagonal argument shows that a new sequence can be found by taking the sequence on the diagonal and changing each individual digit to another one. The new sequence differs in at least one place from every element on the list, so the new sequence cannot be on the list. Therefore, such an enumeration cannot exist.

This is illustrated for binary sequences in this diagram:

Diagonal argument

Source: Jochen Burghardt, via Wikimedia Commons

It’s fairly common to show this argument without much further elaboration, but there are a few problems with doing so:

  • We’re using infinite sequences of digits, not numbers.
    • Equality between sequences is defined by having all elements coincide.
  • We assume we have an enumeration of sequences to which the argument applies. The contents of the enumeration are a mystery.
  • We have no idea which sequences are rational numbers, or if we’d construct one by applying the diagonal argument.

Equality

The purpose of the diagonal argument is to produce a new sequence which was not previously enumerated. The sequence is different in all positions, but what we actually want is equality with respect to the base. In base ten, we have the peculiar identity that 0.\overline{9} = 1. This means that if the diagonal argument (applied to base ten sequences) constructs a new sequence with the digit 9 repeating forever, it might be equivalent to a sequence which was already in the list:

Code 
diagData = rowsOmega [
    [1, 2, 3, 4, 5, 6],
    [9, 2, 4, 8, 3, 7],
    [2, 2, 8, 2, 2, 2],
    [2, 3, 9, 3, 9, 9],
    [9, 4, 9, 4, 9, 4],
    [8, 1, 2, 5, 7, 9]
  ]
  [2, 3, 9, 4, 0, 0]

renderTable (displayDiagRows [Omega, RN 3]
  (numberColumn <> diagBox' 5 <> ellipsisColumn)) diagData
Sequence 0 1 2 3 4 5 ...
0 1 2 3 4 5 6 ...
1 9 2 4 8 3 7 ...
2 2 2 8 2 2 2 ...
3 2 3 9 3 9 9 ...
4 9 4 9 4 9 4 ...
5 8 1 2 5 7 9 ...
... ... ... ... ... ... ... ...
ω 2 3 9 4 0 0 ...

A case in which the diagonal argument could construct a number already on the list.

In the above table, sequence 3 is assumed to continue with 9’s forever. The new sequence ω comes from taking the red digits along the diagonal and mapping each digit to the next one (mod ten). In the enumeration given, the diagonal continues with 9’s forever, so we end up with 0’s forever in ω.

Picking a Sequence and Ensuring Rationals

“No problem, just pick another enumeration,” you might say. Indeed, the example given relies on a simple function and an enumeration to which it is particularly ill-suited.

Instead, let’s focus on something we can do. Instead of assuming we have all irrational numbers listed out already, let’s start smaller. As of last post, we already have several ways to enumerate all rational numbers between 0 and 1. We can take this enumeration and convert each rational number to positional expansions in a base. Then after applying the diagonal argument, the resulting quantity should be an irrational number.

For convenience, we’ll use binary expansions of rationals as our sequences. That way, to get a unique sequence on the diagonal, we only have to worry about changing “0”s to “1”s (and vice versa). Since we have less flexibility in our digits, it also relieves us from some of the responsibility of finding a “good” function, like in the decimal case. However, it’s still possible the argument constructs a number already equal to something on the list.

Into Silicon

Before going any further, let’s write a function for applying the diagonal argument to a list of binary sequences. This can be implemented in Haskell fairly easily:

diagonalize :: [[Int]] -> [Int]
                 -- pair each sequence with its index
diagonalize xs = let sequences = zip [0..] xs in
                 -- read out the red diagonal
                 let diagonal  = map (\(n, s_n) -> s_n !! n) sequences in
                 -- map 0 to 1 and vice versa
                 map (1 -) diagonal
-- or in point-free form
-- diagonalize    = map (\(x,y) -> 1 - (y !! x)) . zip [0..]

Nothing about this function is specific to “binary sequences”, since Int contains values other than 1 and 0. It’s just more intuitive to work with them instead of “True” and “False” (since Bool actually does have 2 values). You can replace (1 -) with not to get a similar function for the type Bool.

We also need a function to get a rational number’s binary expansion. This is simple if you recall how to do long division. We try to divide the numerator by the denominator, “emit” the quotient as part of the result list, then continue with the remainder (and the denominator is unchanged). It’s not quite that simple, since we also need to “bring down” more zeroes. In binary, we can add more zeroes to an expansion by just multiplying by 2.

binDiv :: Int -> Int -> [Int]
-- Divide n by d; q becomes part of the result list
-- The rest of the list comes from doubling the remainder and keeping d fixed
binDiv n d = let (q,r) = n `divMod` d in q:binDiv (2*r) d

x = take 10 $ binDiv 1 3
y = take 10 $ binDiv 1 5

putStrLn $ "x = 1 / 3 = 0." ++ (tail x >>= show) ++ "..."
putStrLn $ "y = 1 / 5 = 0." ++ (tail y >>= show) ++ "..."
x = 1 / 3 = 0.010101010...
y = 1 / 5 = 0.001100110...

This function gives us the leading 0 (actually the integer part of the quotient of n by d), but we can peel it off by applying tail.

Since we intend to interpret these sequences as binary numbers, we might as well also convert this into a form we recognize as a number. All we need to do is take a weighted sum of each sequence by its binary place value.

fromBinSeq :: Int -> [Int] -> Double
               -- Construct a list of place values starting with 1/2
fromBinSeq p = let placeValues = (tail $ iterate (/2) 1) in
               -- Convert the sequence to a type that can multiply with
               -- the place values, then weight, truncate, and sum.
               sum . take p . zipWith (*) placeValues . map fromIntegral

oneFifth = fromBinSeq 64 $ tail $ binDiv 1 5

print oneFifth
0.2

The precision p here is mostly useless, since we intend to take this to as far as Double will go. p = 100 will do for most sequences, since it’s rare that we’ll encounter more than a few zeroes at the beginning of a sequence.

Some Enumerations

Now, for the sake of argument, let’s look at an enumeration that fails. Using the tree of binary fractions from the last post, we use a breadth-first search to create a list of terminating binary expansions.

Tree of binary fractions, as the tree of terminating binary expansions.
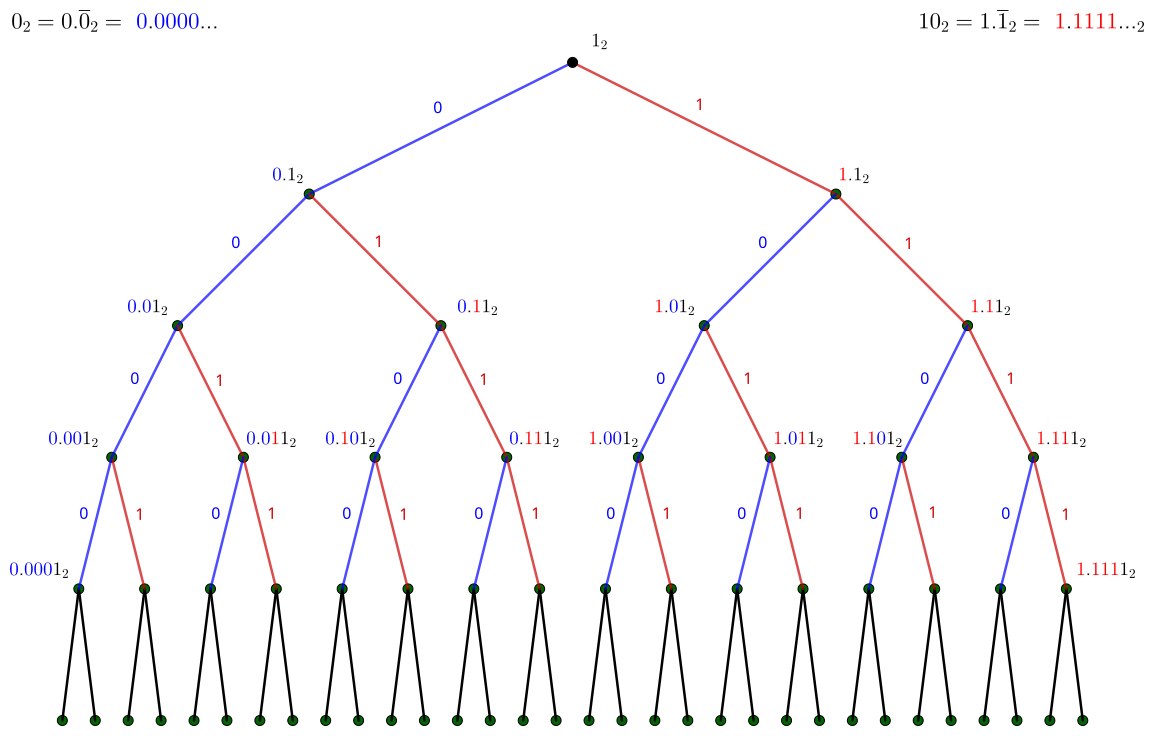
We perform a BFS on the left subtree to obtain the values between 0 and 1.
-- Data class for a labelled sequence
data LabelledSeq a b = LS a [b] deriving Functor
-- Create a labelled binary sequence by dividing n into d and tagging it with "n/d"
binSeqLabelled (n, d) = LS (show n ++ "/" ++ show d) (tail $ binDiv n d)
-- Build a new diagonalize function to work over labelled sequences
lsify diagonalize = diagonalize . map (\(LS _ y) -> y)

-- Extract the left subtree (i.e., the first child subtree)
badDiag diagonalizeLS = let (Node _ (tree:__)) = binFracTree in
          diagonalizeLS $ map binSeqLabelled $ bfs tree
Code 
-- Helper functions for drawing tables
buildDiagTable m = (rowsOmegaLabelled "Fraction" . take m . map (\(LS s y) -> (s, y))) <*> lsify diagonalize
renderDiagTable diagf n = renderTable
  (displayDiagRows []
    (numberColumn <> labelColumn "Fraction" <> diagBox' (n - 1) <> ellipsisColumn)) $
  diagf (buildDiagTable n)

renderDiagTable badDiag 8
Sequence Fraction 0 1 2 3 4 5 6 7 ...
0 1/2 1 0 0 0 0 0 0 0 ...
1 1/4 0 1 0 0 0 0 0 0 ...
2 3/4 1 1 0 0 0 0 0 0 ...
3 1/8 0 0 1 0 0 0 0 0 ...
4 3/8 0 1 1 0 0 0 0 0 ...
5 5/8 1 0 1 0 0 0 0 0 ...
6 7/8 1 1 1 0 0 0 0 0 ...
7 1/16 0 0 0 1 0 0 0 0 ...
... ... ... ... ... ... ... ... ... ...
ω 0 0 1 1 1 1 1 1 ...

Computing the diagonal sequence, it quickly becomes apparent that we’re going to keep getting “0”s along the diagonal. This is because we’re effectively just counting in binary some number of digits to the right. The length of a binary expansion grows logarithmically, but going down the diagonal is a linear process. In other words, we can’t count fast enough by just adding 1 (or adding any number, really).

Even worse than this, we get a sequence which is equal to sequence 1 as a binary expansion. We can’t even rely on the diagonal argument to give us a new number that isn’t equal to a binary fraction.

Stern-Brocot Diagonal

The Stern-Brocot tree contains more than just binary fractions, so we’re bound to encounter more than “0” forever when running along the diagonal. Again, looking at the left subtree, we can read off fractions between 0 and 1.

Stern-Brocot tree

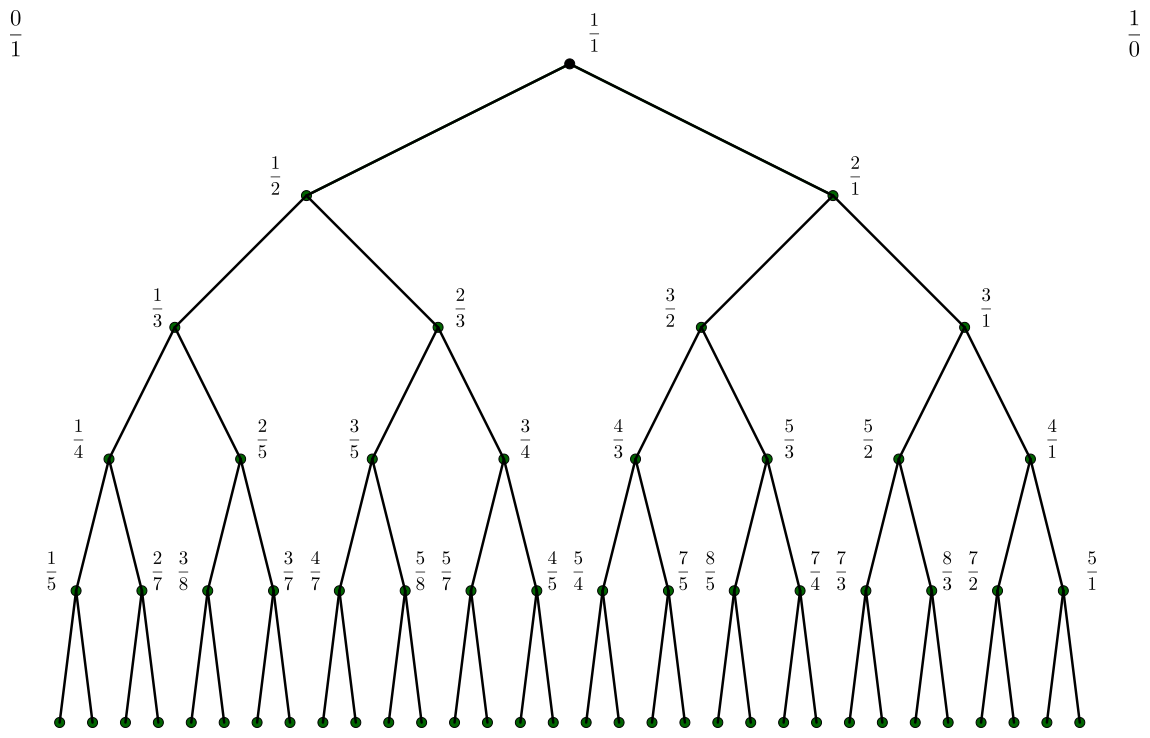
We end up with the following enumeration:

-- Extract the left subtree (i.e., the first child subtree)
sbDiag diagonalizeLS = let (Node _ (tree:__)) = sternBrocot in
          diagonalizeLS $ map binSeqLabelled $ bfs tree

renderDiagTable sbDiag 8
Sequence Fraction 0 1 2 3 4 5 6 7 ...
0 1/2 1 0 0 0 0 0 0 0 ...
1 1/3 0 1 0 1 0 1 0 1 ...
2 2/3 1 0 1 0 1 0 1 0 ...
3 1/4 0 1 0 0 0 0 0 0 ...
4 2/5 0 1 1 0 0 1 1 0 ...
5 3/5 1 0 0 1 1 0 0 1 ...
6 3/4 1 1 0 0 0 0 0 0 ...
7 1/5 0 0 1 1 0 0 1 1 ...
... ... ... ... ... ... ... ... ... ...
ω 0 0 0 1 1 1 1 0 ...

When expressed as a decimal, the new sequence corresponds to the value 0.12059395276… . Dually, its continued fraction expansion begins [0; 8,3,2,2,1,2,12, …]. While the number is (almost) certainly irrational, I have no idea whether it is algebraic or transcendental.

Pairs, without repeats

We have a second, similar enumeration given by allRationalsMap in the previous post. We’ll need to filter out the numbers greater than 1 from this sequence, but that’s not too difficult since we’re already filtering out repeats.

-- Only focus on the rationals whose denominator is bigger
arDiag diagonalizeLS = let rationals01 = filter (uncurry (<)) allRationals in
         diagonalizeLS $ map binSeqLabelled rationals01

renderDiagTable arDiag 8
Sequence Fraction 0 1 2 3 4 5 6 7 ...
0 1/2 1 0 0 0 0 0 0 0 ...
1 1/3 0 1 0 1 0 1 0 1 ...
2 1/4 0 1 0 0 0 0 0 0 ...
3 2/3 1 0 1 0 1 0 1 0 ...
4 1/5 0 0 1 1 0 0 1 1 ...
5 1/6 0 0 1 0 1 0 1 0 ...
6 2/5 0 1 1 0 0 1 1 0 ...
7 3/4 1 1 0 0 0 0 0 0 ...
... ... ... ... ... ... ... ... ... ...
ω 0 0 1 1 1 1 0 1 ...

This new sequence has a decimal expansion equivalent to 0.24005574958… (continued fraction expansion begins [0; 4, 6, 28, 1, 1, 5, 1, …]). Again, this is probably irrational, since WolframAlpha has no idea on whether a closed form exists.

The Diagonal Transform

Why stop with just one? This new number can just be tacked onto the beginning of the list. Then, we re-apply the diagonal argument to obtain a new number. And so on ad infinitum.

transform :: [[Int]] -> [[Int]]
-- Emit the new diagonal sequence, then recurse with the new sequence
-- prepended to the original enumeration
transform xs = let ds = diagonalize xs in ds:transform (ds:xs)
Code 
transformLS :: [LabelledSeq String Int] -> [LabelledSeq String Int]
-- Emit the new diagonal sequence, then recurse with the new sequence
-- prepended to the original enumeration
transformLS xs = let ds = lsify diagonalize xs in LS "" ds:transformLS (LS "" ds:xs)

-- Prepend and append ellipses, then join the reversed transform sequence to the original
buildTransformTable labelName m xs = DR Ellipsis [] []:table where
  table     = concat [reverse prepended, mainTable, [DR Ellipsis [] []]]
  xs'       = transformLS xs
  prepended = take m $ zipWith (\(LS l x) n -> DR (RN $ -n) [] x) xs' [1..]
  mainTable = zipWith (\(LS l x) n -> DR (RN n) [(labelName, l)] x) xs [0..]

-- Render certain diagonals and rows in the same way
displayTransformRows ns = renderCells (stringCell . showCell) $ ns >>= formatDiag where
  formatDiag (n, f) = [
      markDiagonal n (f . show),
      markRows [RN $ n-1] (f . showCell)
    ]

-- Render diagonal 0 (row -1) as red and diagonal -1 (row -2) as green
renderTransformTable n = renderTable
  (displayTransformRows [(0, redCell), (-1, greenCell)]
    (numberColumn <> labelColumn "Fraction" <> diagBox' (n - 1) <> ellipsisColumn)) .
  buildTransformTable "Fraction" 2

renderTransformTable 8 $ take 8 $ sbDiag id
Sequence Fraction 0 1 2 3 4 5 6 7 ...
... ... ... ... ... ... ... ... ... ...
-2 1 1 1 1 1 0 1 1 ...
-1 0 0 0 1 1 1 1 0 ...
0 1/2 1 0 0 0 0 0 0 0 ...
1 1/3 0 1 0 1 0 1 0 1 ...
2 2/3 1 0 1 0 1 0 1 0 ...
3 1/4 0 1 0 0 0 0 0 0 ...
4 2/5 0 1 1 0 0 1 1 0 ...
5 3/5 1 0 0 1 1 0 0 1 ...
6 3/4 1 1 0 0 0 0 0 0 ...
7 1/5 0 0 1 1 0 0 1 1 ...
... ... ... ... ... ... ... ... ... ...

Using the Stern-Brocot enumeration because I like it better

For completeness’s sake, the decimal expansions of the first few numbers which pop are as follows:

sbDiagSeq = let (Node _ (tree:__)) = sternBrocot in
            transform $ map (tail . uncurry binDiv) $ bfs tree

mapM_ print $ take 10 $ map (fromBinSeq 100) sbDiagSeq
0.12059395276295479
0.9839683315741587
0.39401828609177836
0.7474914867558182
3.876798422930419e-2
0.7802097209903278
0.3215249242021624
0.6795283379777878
0.1938245109955674
0.947203605609322

Does this list out “all” irrational numbers? Not even close. In fact, this just gives us a bijection between the original enumeration and a new one containing our irrationals.

The new numbers we get also depend heavily on the order of the original sequence. This is obvious just by looking at the first entry produced by our two good enumerations. Perhaps if we permuted the enumeration of rationals in all possible ways, we would end up listing all irrational numbers, but we’d also run through all ways of ordering the natural numbers.

The fact that “bad” enumerations exist tells us that it’s not even guaranteed that we don’t collide with any rationals. I conjecture that the good enumerations won’t do so, since we shouldn’t ever encounter an infinite sequence of “0”s or “1”s, and a sequence should eventually differ in at least one position from one already listed.

Almost Involution

Since the function has the same input and output type, you may wonder what happens when it’s applied multiple times. Perhaps it is possible that since \x -> 1 - x is an involution, so too is this new function. Alas, experimentation proves us wrong.

sbDiagSeq2 = transform sbDiagSeq

mapM_ print $ take 10 $ map (fromBinSeq 100) sbDiagSeq2
-- Guesses
mapM_ putStrLn [ "1/2", "1/3", "11/12", "1/8", "57/80", "23/80",
  "55/64", "3/40", "???, possibly 613/896", "249/512" ]
0.5
0.3333333333333333
0.9166666666666666
0.125
0.7124999999999999
0.2875
0.859375
7.5e-2
0.6841517857142857
0.486328125
1/2
1/3
11/12
1/8
57/80
23/80
55/64
3/40
???, possibly 613/896
249/512

The fraction forms of the above numbers are my best guesses. Either way, it only matches for the first two terms before going off the rails.

Even stranger than this distorted reflection is the fact that going through the mirror again doesn’t take us anywhere new:

sbDiagSeq3 = transform sbDiagSeq2

squaresAgree n xs ys = let takeSquare zs = take n $ map (take n) zs in
                       takeSquare xs == takeSquare ys

mapM_ print $ take 10 $ map (fromBinSeq 100) sbDiagSeq3
-- First and third iterates agree
print $ squaresAgree 100 sbDiagSeq sbDiagSeq3
0.12059395276295479
0.9839683315741587
0.39401828609177836
0.7474914867558182
3.876798422930419e-2
0.7802097209903278
0.3215249242021624
0.6795283379777878
0.1938245109955674
0.947203605609322
True

In other words, applying the transform thrice is the same as applying the transform once. Not that this has been shown rigorously in the least – it’s only been tested in a 100x100 square.

Regardless, this semi-involutory behavior is strange and nontrivial. And it’s not limited to this enumeration. For example, the filtered allRationalsMap iterations shows:

arDiagSeq = let rationals01 = filter (uncurry (<)) allRationals in
            transform $ map (tail . uncurry binDiv) rationals01


-- What goes in isn't what comes out
mapM_ print $ take 10 $ map (fromBinSeq 100) $ transform arDiagSeq
-- Guesses
mapM_ putStrLn ["1/2", "1/3", "3/4", "1/6", "7/10", "5/12", "139/160", "13/128", "???, possibly 949/1792", "633/1280"]
-- First and third iterates agree
print $ squaresAgree 100 arDiagSeq (transform $ transform arDiagSeq)
0.5
0.3333333333333333
0.75
0.16666666666666666
0.7
0.41666666666666663
0.8687499999999999
0.1015625
0.5295758928571428
0.49453125
1/2
1/3
3/4
1/6
7/10
5/12
139/160
13/128
???, possibly 949/1792
633/1280
True

Meanwhile, the bad enumeration just gives more binary fractions, but it still doesn’t mean double-transforming returns the original diagonal.

bfDiagSeq = let (Node _ (tree:__)) = binFracTree in
            transform $ map (tail . uncurry binDiv) $ bfs tree

(putStrLn "First diagonal transform: " >>) $
  mapM_ print $ take 10 $ map (fromBinSeq 100) bfDiagSeq
-- Guesses
mapM_ putStrLn ["Guesses", "1/4", "1/1", "1/2", "5/8", "1/16", "25/32", "25/64", "81/128", "49/256", "417/512"]

-- What goes in isn't what comes out
(putStrLn "Second diagonal transform: " >>) $
  mapM_ print $ take 10 $ map (fromBinSeq 100) $ transform bfDiagSeq
-- Guesses
mapM_ putStrLn ["Guesses", "1/2", "1/4", "3/4", "1/8", "11/16", "15/32", "55/64", "15/128", "143/256", "223/512"]

-- First and third iterates agree
print $ squaresAgree 100 bfDiagSeq (transform $ transform bfDiagSeq)
First diagonal transform: 
0.25
1.0
0.5
0.625
6.25e-2
0.78125
0.390625
0.6328125
0.19140625
0.814453125
Guesses
1/4
1/1
1/2
5/8
1/16
25/32
25/64
81/128
49/256
417/512
Second diagonal transform: 
0.5
0.25
0.75
0.125
0.6875
0.46875
0.859375
0.1171875
0.55859375
0.435546875
Guesses
1/2
1/4
3/4
1/8
11/16
15/32
55/64
15/128
143/256
223/512
True

What does it mean that the initial enumeration comes back as a completely different one? Since the new one is “stable” with respect to applying the diagonal transform twice, are the results somehow preferable or significant?

Closing

These questions, and others I have about the products of this process, I unfortunately have no answer for. I was mostly troubled by how rare it is to find people applying the diagonal argument to something to anything other than random sequences.

Random sequences, either by choice or by algorithm (if you can even call them random at that point), are really only good to show how to apply the diagonal argument. Without knowing what the argument is applied to, it’s useless for constructive arguments. It also still remains to be proven that your new sequences are sufficient for the purpose (since I’ve only shown a case in which it fails).

(Recycled) diagrams made in Geogebra.